Negative plus negative is an essential concept in integer addition that many students initially find challenging. Understanding how to add negatives correctly lays a strong foundation for more advanced math skills.
So in this guide, we’ll walk you through the rules for adding two negative numbers, offer simple examples, and share tips to make learning engaging. Perfect for teachers who want to help students gain confidence and master adding with negatives effectively.
Understanding Negative Numbers
Before diving deep into adding negative numbers, it’s important to fully understand what negative numbers are and why they matter:
What Are Negative Numbers?
Negative numbers are numbers less than zero. They are represented with a minus sign (-) in front, such as -1, -5, or -100. Negative numbers are the opposite of positive numbers and are used to describe quantities below a certain point, such as temperatures below zero or debts.
One of the easiest ways to understand negative numbers is to picture a number line:
- Zero is the center point.
- Positive numbers increase as you move to the right.
- Negative numbers increase in magnitude as you move to the left.

Why Do We Use Negative Numbers?
Negative numbers help us describe:
- Temperatures below freezing: For example, -10°C means 10 degrees below zero.
- Financial debt: Owing $20 can be represented as -20.
- Elevation below sea level: Like -50 meters means 50 meters below sea level.
By thoroughly understanding what negative numbers represent and how they work, students will have a stronger foundation for the addition of negative numbers and other related operations.
What Does Negative Plus Negative Mean?
At its core, negative plus negative equals the addition of two numbers both less than zero. For example, what does -5 + (-8) equal? The answer might not be obvious to beginners, but it follows consistent mathematical principles.
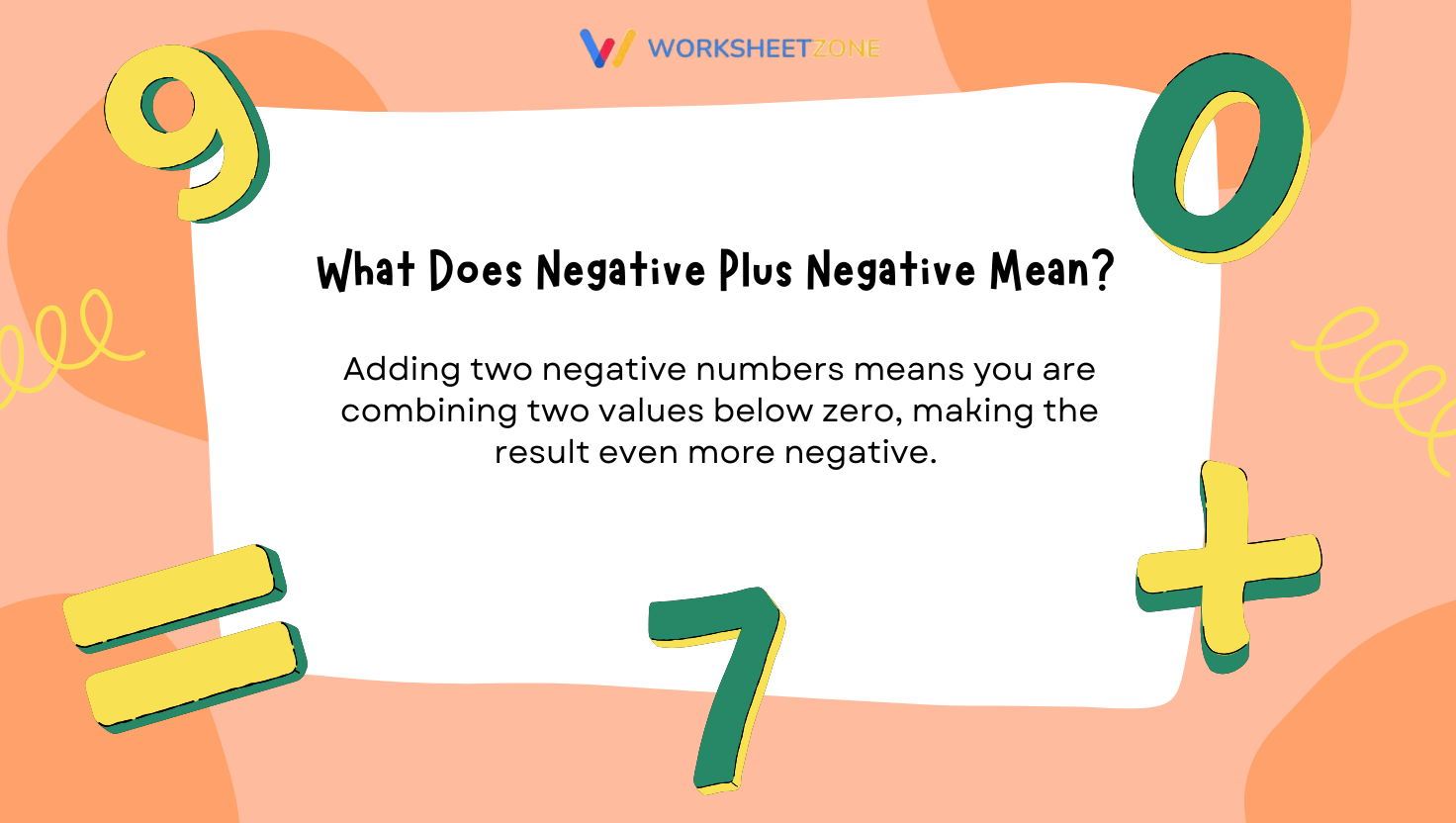
Adding minus numbers means you are combining two values below zero, making the result even more negative. This can be visualized on a number line moving left from zero. Each negative number pulls you further away from zero in the negative direction.
How to Add Negative Integers?
Below is a step-by-step breakdown of how to solve a negative plus negative problem:
Step 1: Identify the Numbers and Their Signs
Before doing any math, carefully identify the numbers involved in the problem. Look for the minus signs that indicate the numbers are negative. This step is essential when adding negative numbers, as it ensures accuracy right from the beginning.

Examples:
- -3 + (-5)
- -7 + (-2)
In each example above, both numbers are negative.
Step 2: Ignore the Negative Signs and Add the Absolute Values
Once you recognize both numbers are negative, ignore their signs temporarily and focus only on their absolute values. The absolute value of a number is how far it is from zero, regardless of direction.

For example:
For -3 + (-5)
→ Absolute values: |–3| = 3, |–5| = 5
→ Add: 3 + 5 = 8
For -7 + (-2)
→ Absolute values: |–7| = 7, |–2| = 2
→ Add: 7 + 2 = 9
By doing this, you’re simplifying the problem to basic addition, helping students learn how to add minus numbers by first stripping away the confusion around negative signs.
Step 3: Attach the Negative Sign to the Result
Now that you’ve added the absolute values, it’s time to apply the correct sign to your answer. Remember the most important adding negative numbers rules:
When a negative plus a negative, the result will always be negative.
So:
- -3 + (-5) = -8
- -7 + (-2) = -9

As we can see, a negative plus negative equals a more negative number. This concept often surprises students, but once they understand that you’re essentially going “deeper into the negatives,” it starts to make sense.
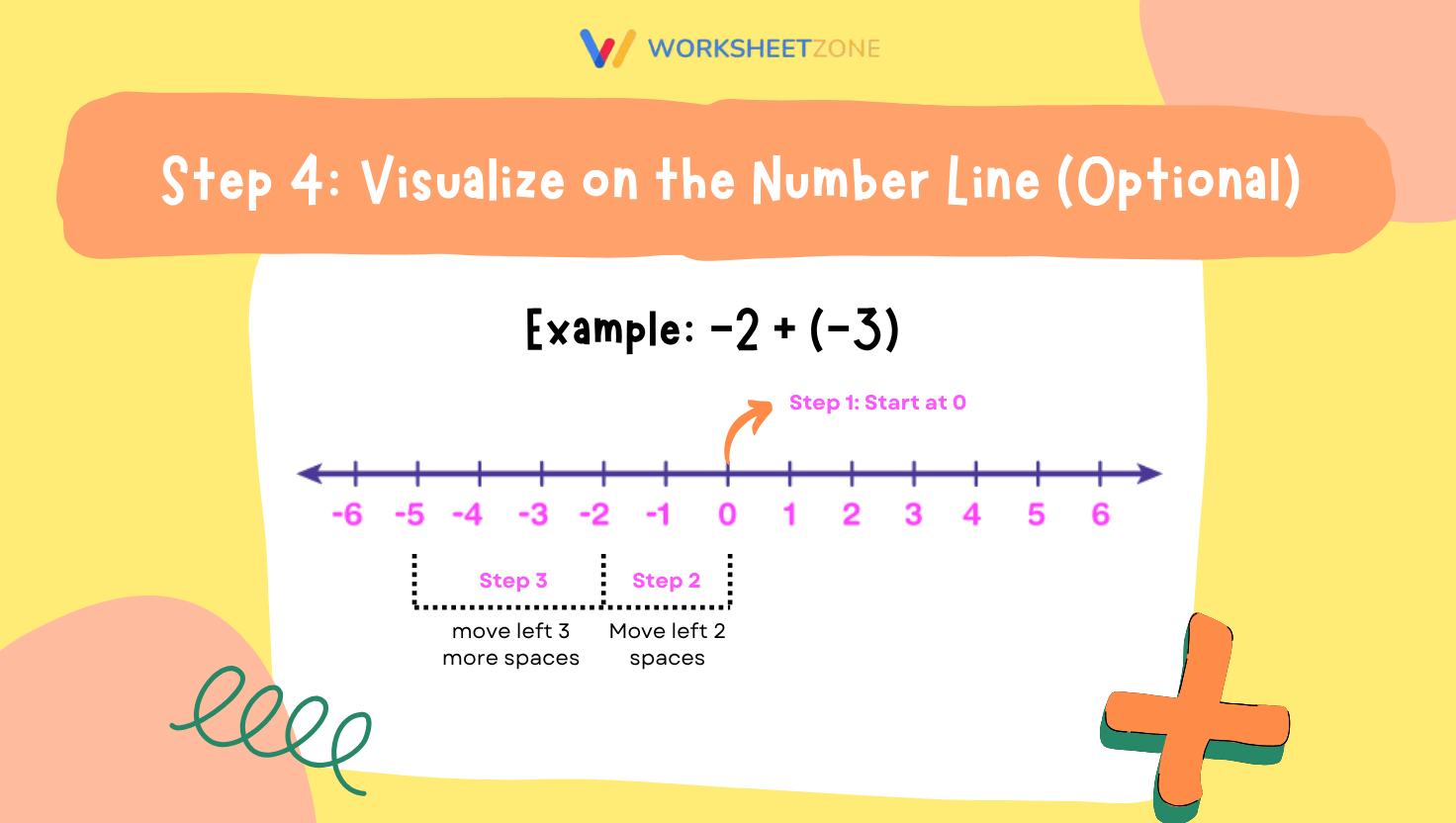
Step 4: Visualize on the Number Line (Optional but Powerful)
For visual learners, using a number line can be a powerful tool to understand adding negatives. Here’s how to do it step-by-step:
- Start at 0.
- Move left the number of units equal to the first negative number.
- From there, move further left the number of units equal to the second negative number.
- Where you land is your final answer.
For example: -2 + (-3)
- Start at 0
- Move left 2 spaces → land on -2
- From -2, move left 3 more spaces → land on -5
So -2 + (-3) = -5
Quick Recap: Rules for Adding Negative Integers
Okay, so you’ve learned all the steps above—now let’s wrap it up with a quick summary:
- When adding negative plus negative, add their absolute values.
- The result will always be negative.
- Think of adding two negatives as moving left on the number line. Every time you add a negative number, you move further left, away from zero.

Let’s Practice! Solved Examples Based on Integers
Now, it’s time to apply that knowledge to real-world problems. Below are some solved examples based on integers:
Example 1:
Problem: -4 + (-6)
Solution:
- Step 1: Identify both numbers as negative.
- Step 2: Add absolute values → 4 + 6 = 10
- Step 3: Final answer is negative → -10
Answer: -4 + (-6) = -10

Example 2:
Problem: -7 + (-3)Solution:
- Step 1: Recognize both numbers are negative integers.
- Step 2: Add absolute values → 7 + 3 = 10
- Step 3: Result is negative → -10
Answer: -7 + (-3) = -10

Example 3:
Problem: -2 + (-9)Solution:
- Step 1: Identify that both are negative integers.
- Step 2: Absolute values: 2 + 9 = 11
- Step 3: Attach the negative sign → -11
Answer: -2 + (-9) = -11

Example 4:
Problem: -12 + (-4)Solution:
- Step 1: Both numbers are negative.
- Step 2: Add their absolute values → 12 + 4 = 16
- Step 3: Add the negative sign → -16
Answer: -12 + (-4) = -16
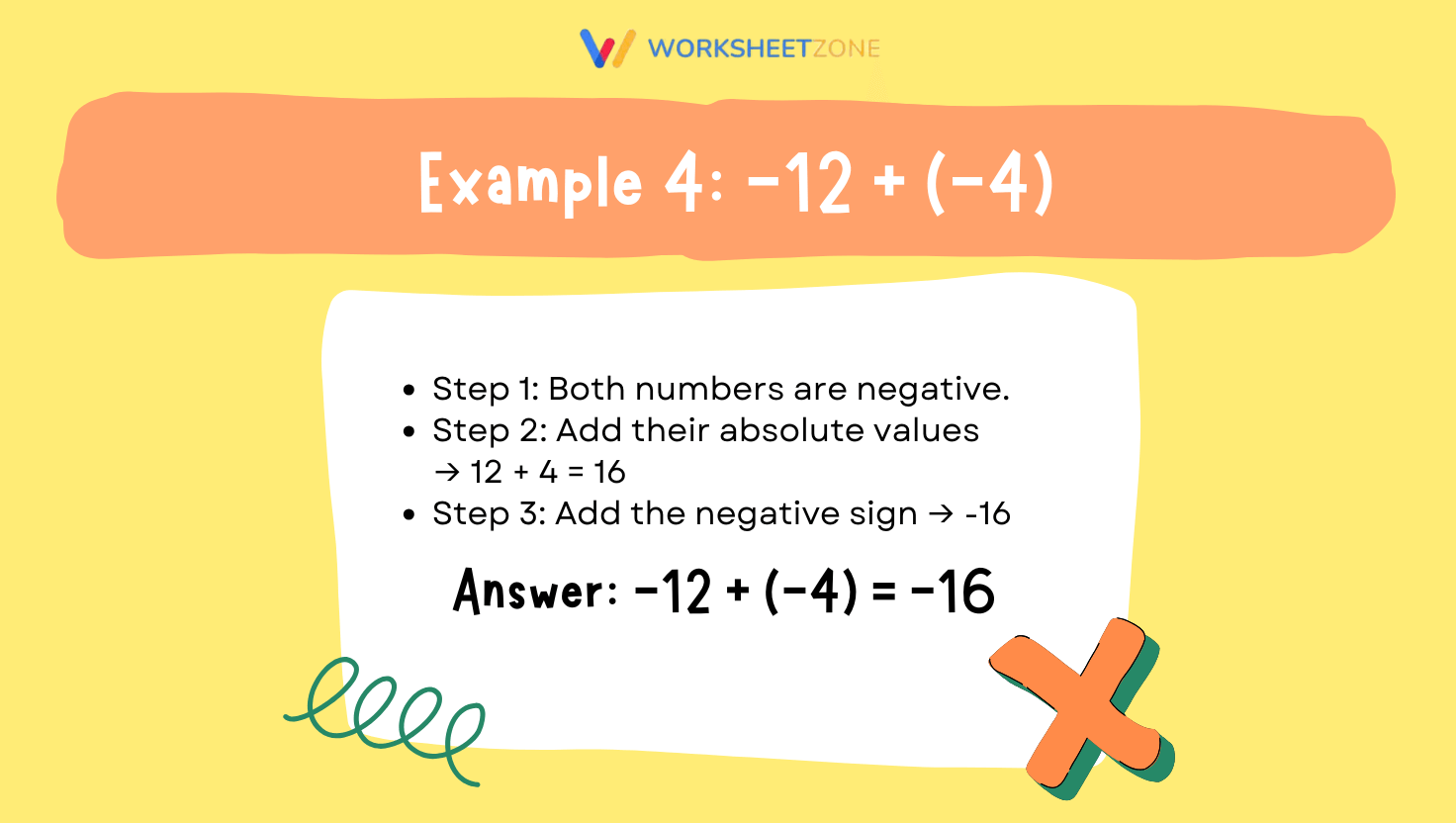
Example 5:
Problem: -15 + (-5)
Solution:
- Step 1: Both integers are negative.
- Step 2: Add absolute values → 15 + 5 = 20
- Step 3: Add a minus sign to the result → -20
Answer: -15 + (-5) = -20
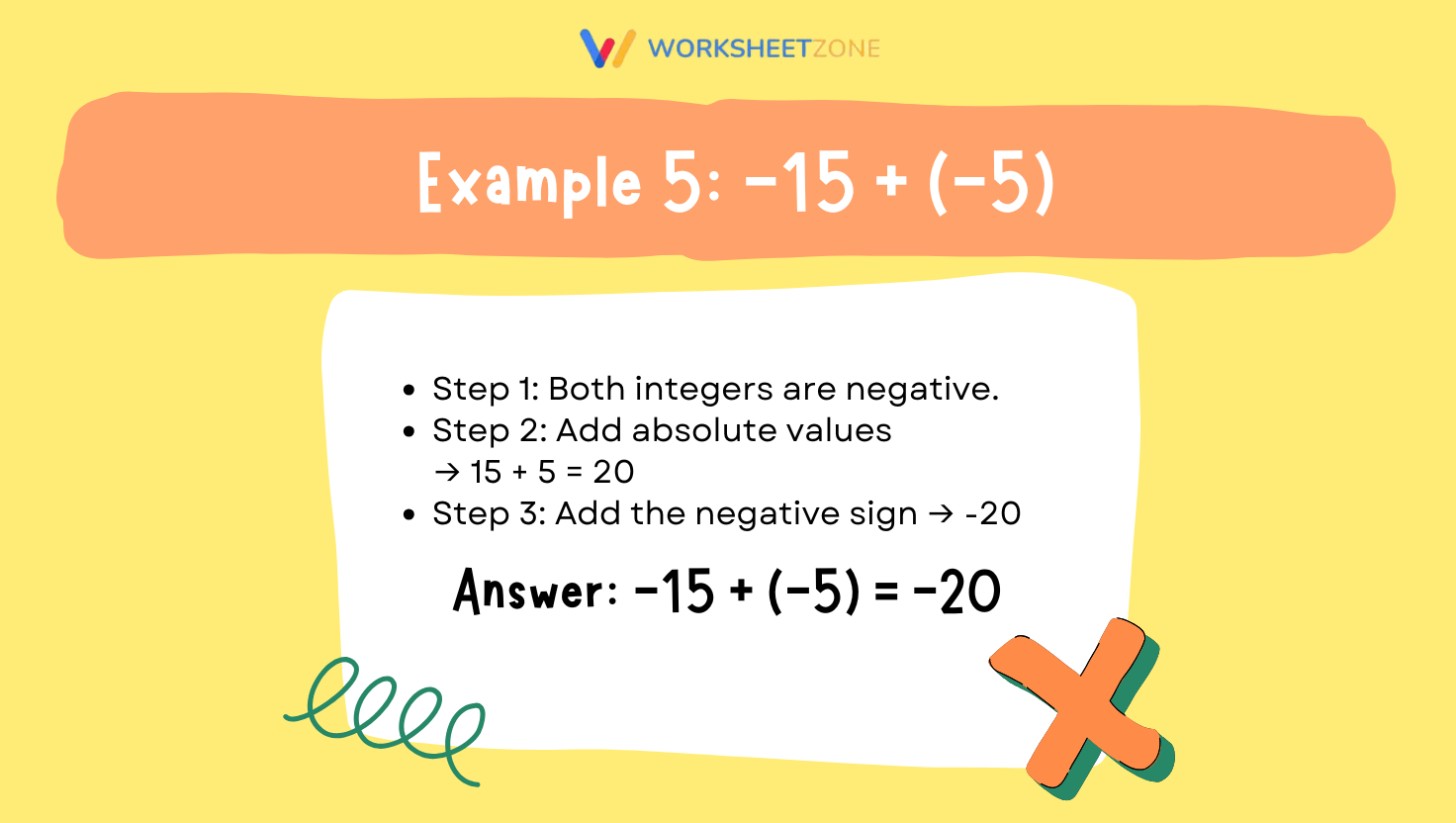
Final Thoughts
Negative plus negative is an important lesson during math because it helps students build a strong foundation in working with integers. Once they understand how to add two negative numbers, their confidence grows and they’re better prepared for more complex concepts ahead.
Want to make this learning process easier? Check out these printable worksheets and interactive activities designed to give your students plenty of practice with adding negative numbers—helping them master the skill while having fun!